Mecanismos de línea recta

 Son aquellos mecanismos en los cuales algún punto de sus eslabones describe una trayectoria recta ya sea aproximada o exacta, nomenclatura que se le da comúnmente en la literatura. Estos mecanismos tuvieron un gran auge a finales del siglo XVIII en la revolución industrial, ya que los pares prismáticos con los que se contaban tenían demasiada holgura y se requería de una mayor precisión para los procesos de fabricación y automatización. A continuación, se describirán los principales mecanismos generadores de trayectorias rectas para seleccionar uno que tenga la capacidad de adaptarse como un mecanismo de propulsión para máquinas caminantes al modificar las longitudes de sus eslabones móviles.

Mecanismo de línea recta de Watt

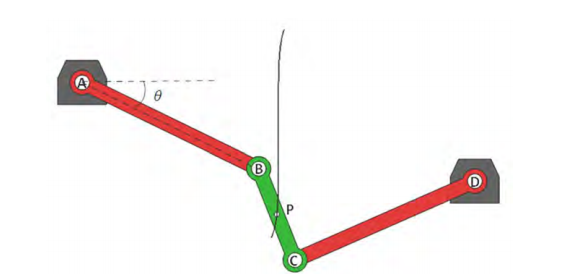
Este mecanismo, patentado por James Watt en 1784, es considerado como de línea recta aproximada, es un mecanismo de cuatro barras o eslabones que cuenta con cuatro articulaciones rotacionales nombradas A, B, C y D las cuales dan el nombre a cada uno de los eslabones. Los eslabones AB y CD que se articulan rotacionalmente al eslabón fijo (tierra), tienen la misa longitud, mientras que el eslabón BC que acopla a estos dos eslabones, las dimensiones de cada uno de los eslabones de este mecanismo que se consideraron para este estudio se muestran en la Tabla. El punto medio P del eslabón BC describe una línea recta aproximada.

Este mecanismo se analiza para ver si se puede adaptar a un mecanismo de propulsión para máquinas caminantes por lo que es necesario que además de poder describir trayectorias rectas, también pueda describir curvas con respecto a un eje de rotación y así cumplir con el principio básico de desplazamiento; para lograr esto se modificaron las longitudes de sus eslabones para ver si es posible que describan trayectorias curvas.

Se aprecia el Caso I, cuando  observando que al reducir y aumentar la longitud de estos eslabones, el centro P del eslabón BC describe una trayectoria curva, pero con centro de rotación variable, se observa el Caso II, cuando, observando el centro P del eslabón BC también describe una trayectoria curva con centro de rotación variable; en el Caso III se aumenta la longitud del eslabón BC obteniendo sólo una inclinación en la recta que describe el punto P, como se aprecia y por último, se observa el tipo de trayectoria que se obtiene al reducir el tamaño del eslabón BC, que es una inclinación para el lado opuesto al caso anterior. Estas combinaciones no le darían al mecanismo de Watt la capacidad de rotar con facilidad con respecto a un eje de rotación fijo además de que para trazar una curva se requiere una gran diferencia entre la longitud de sus eslabones AB y CD.

Mecanismo de línea recta de Roberts
El mecanismo de Roberts, es un mecanismo de cuatro barras, el cual también cuenta con cuatro articulaciones rotacionales nombradas A, B, C y D, como se aprecia. En este mecanismo la longitud de los eslabones AB y CD son iguales, mientras que el eslabón acoplador tiene la forma de un triángulo isósceles con el punto P que describe una trayectoria recta aproximada durante una parte del movimiento, mientras que el resto de la trayectoria descrita es curva. Esta trayectoria curva tiene la desventaja de que para realizarla se debe pasar por posiciones singulares además de que el punto P pasa por las articulaciones fijas A y D. Las dimensiones empleadas en esta configuración del mecanismo se aprecian en la Tabla.

Al modificar las longitudes de los eslabones AB o CD de acuerdo al Caso I descrito en la Tabla, se obtiene una inclinación en la recta descrita por el punto P, como se aprecia. Otra modificación planteada es variar las longitudes del triángulo formado por el acoplador de acuerdo al Caso II descrito en la Tabla, para lo cual se obtiene una pequeña curvatura, pero solamente en una pequeña parte de la trayectoria como se aprecia, por lo que no es posible emplear el mecanismo, ya que no puede girar con respecto a un eje de rotación de forma fácil, lo cual dificultaría cumplir con el principio básico de desplazamiento. Otra opción es emplear la parte curva de la trayectoria que describe el mecanismo, pero es difícil cambiar el centro de rotación a uno que difiera mucho del original, además de las posiciones singulares mencionadas previamente.

mecanismos de línea recta de Chebyschev

Éste mecanismo también se compone de cuatro barras que se unen mediante cuatro articulaciones rotacionales denominadas A, B, C y D las cuales dan nombre a los eslabones, los eslabones AB y CD se encuentran articulados a tierra y tienen la misma longitud, mientras que el centro del eslabón acoplador BC describe una trayectoria recta aproximada durante una etapa del movimiento y una trayectoria curva en el desplazamiento restante, esto se puede apreciar, caso para el cual se emplean las longitudes mostradas en la Tabla.

Para cumplir con el principio básico de desplazamiento se tratan cuatro casos en los cuales se modifican las dimensiones de los eslabones de acuerdo a la Tabla, iniciando con el Caso I, en el cual se modifican las longitudes de los eslabones AB y CD, encontrando que se pueden describir trayectorias curvas con centro de rotación perpendicular a la trayectoria recta descrita. Como se observa en la Figura.

En el Caso II se modifican las longitudes de los eslabones AB y CD del valor inicial, pero la longitud de ambos eslabones siempre permanece igual, obteniendo trayectorias curvas, pero con centro variable, hasta llegar al mecanismo de Watt, para el Caso III solamente se aumenta la longitud de eslabón acoplador BC, encontrando que se puede describir trayectorias curvas con centro constante, como se describe, en donde se llegan hasta las dimensiones de los eslabones que permiten convertir a éste en un mecanismo de triple manivela; por último, en el caso IV se reduce la longitud del eslabón BC en donde se obtiene trayectorias rectas aproximadas pero con segmentos más cortos como se aprecia.

Mecanismo de línea recta de Hoeken

Es un mecanismo de cuatro barras con cuatro articulaciones rotacionales llamadas A, B, C y D las cuales dan nombre a los eslabones, la manivela AB y el balancín CD se encuentran conectados a tierra, mientras que el punto P que es una extensión del eslabón acoplador BC describe una línea recta aproximada en la sección inferior de la trayectoria. Las dimensiones empleadas en este mecanismo se muestran en la Tabla. Este mecanismo tiene la ventaja de que la velocidad en la trayectoria recta es casi constante.

En este mecanismo se analizaron cinco casos, los cuales modifican las longitudes de los eslabones AB, BC, CP y AD con las relaciones que se muestran, para ver si es posible que el mecanismo describa trayectorias curvas. 

En el Caso I, la longitud del eslabón AB varía, encontrando que al aumentar la longitud de éste se obtiene dos curvas de radio muy grande por lo que apenas pueden apreciarse, como se muestra en la Figura; en el Caso II, al modificar la longitud del eslabón BC, se observa que describen trayectorias curvas con centro variable como la mostrada; para el Caso III, se aumenta la longitud del segmento CP, encontrando que obtiene también trayectorias curvas con centro variable como se aprecia, lo cual no facilita que el mecanismo cumpla con el principio básico de desplazamiento; el Caso IV reduce la distancia entre el segmento CP lo cual también describe una trayectoria curva con centro variable como se aprecia, y por último se analizó el Caso V, en el cual se modifica la longitud del eslabón CD, obteniendo como resultado la descripción de dos trayectorias aproximadamente curvas como se aprecia, esta curva descrita no tiene la misma dirección que la trayectoria recta descrita por este mecanismo.

Mecanismos de línea recta de Scott Russel o Isósceles

Hasta ahora se han estudiado mecanismos de cuatro barras con articulaciones rotacionales, que solamente pueden describir trayectorias rectas aproximadas. En esta sección se estudia un mecanismo con tres articulaciones rotacionales y una prismática que puede describir una trayectoria recta exacta. 

Este mecanismo se llama Scott Russel y es un mecanismo de cuatro eslabones. Cuenta con tres articulaciones rotacionales nombradas A, B y C, y una articulación prismática llamada D, como se aprecia. 

Se puede apreciar como el punto P puede describir trayectorias rectas exactas, además de que se forma un triángulo isósceles entre las articulaciones ABCA y entre los puntos ABPA, esto se debe a que la longitud del eslabón AB es igual a la longitud del eslabón BC, así como a la longitud del segmento BP, esto le permite con una parte del principio básico de desplazamiento, pero para que este pueda girar con respecto a un centro de rotación se comienza por analizar los casos de modificación descritos en la Tabla; en el Caso I se reduce la longitud del eslabón AB, obteniendo arcos como los mostrados en la Figura, también se analiza el Caso II donde se modifica la longitud del eslabón BC, en el cual se obtiene un arco rotado mostrado en la Figura, ya que no tiene la misma orientación que la recta; también se analiza el Caso III en el cual se aumenta la longitud del segmento BP, lo cual genera un arco cóncavo con respecto al punto C, Figura; por último se analiza el Caso IV, en el cual se disminuye la longitud del segmento BP lo que genera un arco convexo con respecto al punto C.

Las longitudes empleadas en los eslabones del mecanismo para trazar una línea recta, así como la descripción de los casos analizados se pueden observar en la Tabla. Este mecanismo puede cumplir con el principio básico de desplazamiento, por lo que se puede emplear como mecanismo de propulsión para máquinas caminantes, sin embargo, tiene la desventaja de que cuando describe líneas rectas y en el Caso IV el punto P se cruza con otros eslabones y como los eslabones son sólidos, esto representa un serio problema en el diseño.

Mecanismos de línea recta exacta de Hart
Para que un mecanismo pueda describir trayectorias rectas exactas con articulaciones rotacionales se requiere que tenga al menos seis eslabones, el mecanismo de Hart es un mecanismo de seis eslabones con siete articulaciones rotacionales nombradas A, B, C, D, E, F y G, estas articulaciones les dan nombre a los eslabones. Para que el punto P describa una línea recta exacta como la que se muestra, se deben cumplir las siguientes relaciones entre los eslabones y por último se deben cumplir las relaciones de longitud.

Las longitudes de los eslabones empleadas se muestran en la Tabla, en ésta misma se muestran los casos en los cuales la variación de las longitudes de los eslabones genera que el punto P describa trayectorias curvas. 

El Caso I en donde se reduce la longitud del eslabón DE, se observa que el punto P describe arcos con centro de rotación constante en la parte inferior como se aprecia en la Figura; para el Caso II se aumenta la longitud de eslabón DE y el punto P describe otra trayectoria con centro de rotación constante pero en esta ocasión en la parte superior del mecanismo como se muestra en la Figura; en el Caso III se aumenta la longitud entre las articulaciones A y B teniendo como resultado que el punto P, describa una trayectoria curva como se aprecia en la Figura, similar a la descrita en el caso II; finalmente en el caso IV se reduce la distancia entre los eslabones AB con lo que se obtiene una trayectoria curva con centro de rotación variable descrita por el punto P, como se aprecia. 

El mecanismo de Hart tiene la capacidad de describir tanto trayectorias curvas como trayectorias rectas exactas con lo cual podría cumplir con el principio básico de desplazamiento, con la desventaja de que las trayectorias rectas y curvas descritas por este mecanismo se encuentran en diferentes direcciones a las trayectorias deseadas.

Mecanismos de línea recta exacta de Peaucellier- Lipkin

Por último, analizaremos el mecanismo Peaucellier-Lipkin, que es un mecanismo de ocho barras que cuenta con seis articulaciones rotacionales llamadas A, B, C, D, E y F las cuales les dan el nombre a los eslabones que lo conforman. En este caso la articulación F es la que describe trayectorias rectas exactas, como la que se muestra en la Figura; para describir trayectorias rectas exactas se deben cumplir las siguientes relaciones entre las longitudes de sus eslabones.

Las dimensiones empleadas para la configuración del mecanismo Peaucellier-Lipkin analizado se pueden apreciar en la Tabla; en esta tabla también se aprecian los cuatro casos analizados para comprobar si el mecanismo puede cumplir con el principio básico de desplazamiento. 

En el Caso I se reduce la longitud del eslabón BC, observando que la articulación F puede describir trayectorias curvas con centro de rotación constante, el cual se ubica a la derecha de esta articulación como se puede apreciar en la Figura; en el Caso II se aumenta el tamaño del eslabón BC, como se aprecia en la Tabla, con lo que se obtienen arcos con centro de rotación constante, el cual se ubica a la izquierda de esta articulación como se aprecia en la Figura. Es importante mencionar que en los dos casos estudiados hasta el momento las trayectorias curvas descritas por el punto F tienen la misma orientación, a diferencia de lo obtenido en la mayoría de los mecanismos previamente estudiados, ya que el centro de las curvas obtenidas se encuentra alineado con el eslabón AB. En el Caso III de estudio se modifican las longitudes de los eslabones AD y AE obteniendo curvas con centro variable en el que la mitad de la curva tiene centro a la izquierda de la articulación F, mientras que la otra mitad de la curva tiene centro a la derecha de esta articulación, Figura; para concluir se analiza el Caso IV en donde se modifica el rombo formado por las articulaciones CDFEC, Figura, en donde dos lados cambian de valor en la longitud, con lo que se obtiene la descripción de trayectorias curvas con centro variable.

Selección del mecanismo de línea recta

Después de analizar diversos mecanismos de línea recta aproximada y exacta para comprobar cuáles tienen la capacidad de cumplir con el principio básico de desplazamiento y poder aplicarlos como mecanismos de propulsión para máquinas caminantes, se realiza un análisis de siete de las principales ventajas y desventajas que presenta cada mecanismo que permite realizar una selección del mecanismo a emplear, como se aprecia en la Tabla. 

En base a las ventajas y desventajas se pueden seleccionar dos mecanismos: el mecanismo de Scott Russel y el mecanismo Peaucellier-Lipkin, el primero tiene la gran ventaja de ser un mecanismo simple ya que solamente tiene cuatro eslabones, pero tiene como desventajas que presenta posiciones singulares, además de que el punto de trazo cruza por elementos solidos lo cual podría ser un gran problema para el diseño. El mecanismo de Peaucellier-Lipkin solamente tiene la desventaja de que cuenta con ocho eslabones, pero puede cumplir con el principio básico de desplazamiento, además de que el punto de trazo no interfiere con otros elementos ni presenta singularidades. En base a este análisis se propone el mecanismo Peaucellier-Lipkin como la base de un mecanismo de propulsión para máquinas caminantes ya que es el que presenta las mayores ventajas en comparación con los otros mecanismos analizados.